「实验记录」Verilog 实现的 5-bit 华莱士树加法器

利用全加器、串行进位加法器依次设计七输入 3-bit 华莱士树加法器、十五输入 4-bit 华莱士树加法器和三十一输入 5-bit 华莱士树加法器并设计 TestBench 检查输出波形。

一、实验内容

设计一个输入数为 31 的 5-bit 华莱士树加法器。

二、设计过程

根据前序实验，我们知道华莱士树加法器具有良好的可拓展性，多位的华莱士树加法器可以通过低位华莱士树加法器和多位串行加法器构成，故首先设计七输入 3-bit 华莱士树加法器作为后续实验的基础。

七输入 3-bit 华莱士树加法器由两个并行的全加器与一个 2-bit 串行进位加法器组成，将此部分作为模组封装。

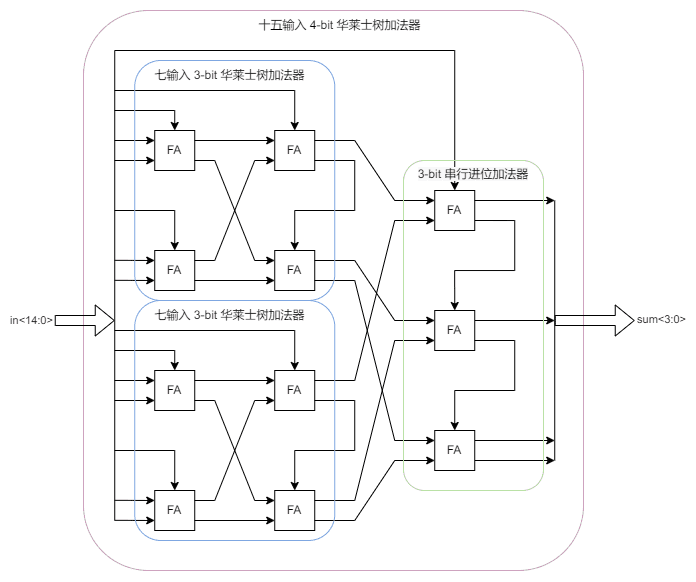十五输入 4-bit 华莱士树加法器由两个七输入 3-bit 华莱士树加法器与一个 3-bit 串行进位加法器组成，将此部分作为模组封装。

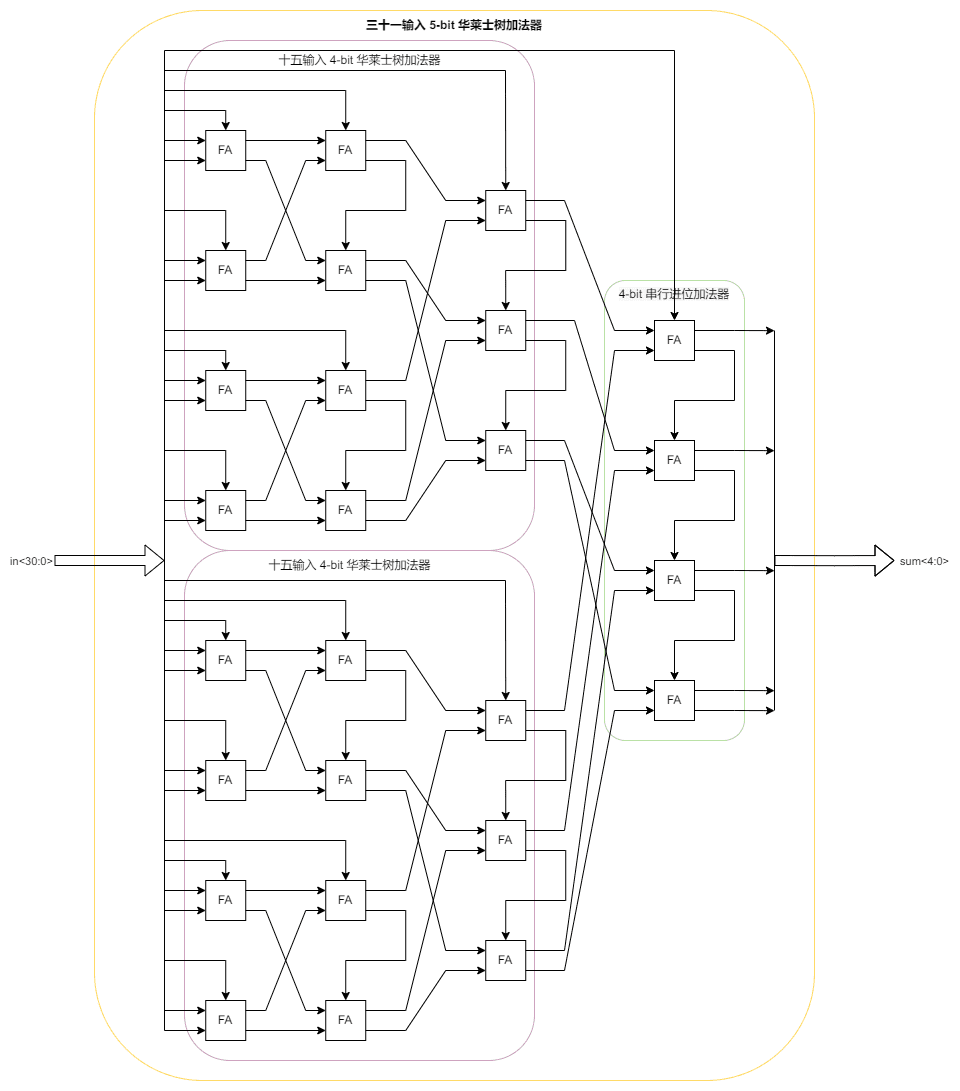三十一输入 5-bit 华莱士树加法器由两个十五输入 4-bit 华莱士树加法器与一个 4-bit 串行进位加法器组成，将此部分作为模组封装。

最后设计 Testbench 激励，为三十一输入 5-bit 华莱士树加法器模组提供合适的信号激励，获得输出波形。

三、核心代码

全加器

module fulladd(sum, c_out, a, b, c_in);

    input a, b, c_in;
    output c_out, sum;
    assign {c_out, sum} = a + b + c_in;

endmodule

本部分是一个基本的 1-bit 全加器，亦是华莱士树加法器和串行进位加法器的基本组成部分，作为基本单元在后续过程中频繁被调用。

七输入 3-bit 华莱士树加法器

module ThreebitWallace(in, sum);

    input [6:0] in;
    output [2:0] sum;
    wire [1:0] s;
    wire [2:0] c;

    fulladd adder0(
        .a(in[0]),
        .b(in[1]),
        .c_in(in[4]),
        .sum(s[0]),
        .c_out(c[0])
    );

    fulladd adder1(
        .a(in[2]),
        .b(in[3]),
        .c_in(in[5]),
        .sum(s[1]),
        .c_out(c[1])
    );

    fulladd adder2(
        .a(s[0]),
        .b(s[1]),
        .c_in(in[6]),
        .sum(sum[0]),
        .c_out(c[2])
    );

    fulladd adder3(
        .a(c[0]),
        .b(c[1]),
        .c_in(c[2]),
        .sum(sum[1]),
        .c_out(sum[2])
    );

endmodule

本部分是一个七输入 3-bit 华莱士树加法器，也是最小的华莱士树加法器，用于构建十五输入 4-bit 华莱士树加法器。本次实验中直接使用了四个全加器构成本部分，后续可以考虑重构为 2-bit 串行进位加法器与两个全加器的组合。

3-bit 串行进位加法器

module ThreebitAdder(sum, c_out, a, b, c_in);

    input [2:0] a, b;
    input c_in;
    output c_out;
    output [2:0] sum;

    assign {c_out, sum} = a + b + c_in;

endmodule 

本部分是一个基于数据流模型的 3-bit 串行进位加法器，用于构建十五输入 4-bit 华莱士树加法器。

十五输入 4-bit 华莱士树加法器

module FourbitWallace(in, sum);

    input [14:0] in;
    output [3:0] sum;
    wire [2:0] sum_0, sum_1;

    ThreebitWallace TW0(
        .in(in[6:0]),
        .sum(sum_0[2:0])
    );

    ThreebitWallace TW1(
        .in(in[13:7]),
        .sum(sum_1[2:0])
    );

    ThreebitAdder TA0(
        .c_in(in[14]),
        .a(sum_0[2:0]),
        .b(sum_1[2:0]),
        .sum(sum[2:0]),
        .c_out(sum[3])
    );

endmodule

本部分是一个十五输入 4-bit 华莱士树加法器，由两个七输入 3-bit 华莱士树加法器与一个 3-bit 串行进位加法器组成，用于构建三十一输入 5-bit 华莱士树加法器。

4-bit 串行进位加法器

module FourbitAdder(sum, c_out, a, b, c_in);

    input [3:0] a, b;
    input c_in;
    output c_out;
    output [3:0] sum;

    assign {c_out, sum} = a + b + c_in;

endmodule

本部分是一个基于数据流模型的 4-bit 串行进位加法器，用于构建三十一输入 5-bit 华莱士树加法器，至此所有基础设施已经构建完毕。

三十一输入 5-bit 华莱士树加法器

module FivebitWallace(in, sum);

    input [30:0] in;
    output [4:0] sum;
    wire [3:0] sum_0, sum_1;

    FourbitWallace FW0(
        .in(in[14:0]),
        .sum(sum_0[3:0])
    );

    FourbitWallace FW1(
        .in(in[29:15]),
        .sum(sum_1[3:0])
    );

    FourbitAdder TA0(
        .c_in(in[30]),
        .a(sum_0[3:0]),
        .b(sum_1[3:0]),
        .sum(sum[3:0]),
        .c_out(sum[4])

    );

endmodule

本部分是一个三十一输入 5-bit 华莱士树加法器，即本次实验的设计目标，由十五输入 4-bit 华莱士树加法器与一个 4-bit 串行进位加法器。至此已基本完成本次实验的核心设计，只需撰写 TestBench 文件用于提供激励即可。

TestBench

`timescale 1ns/1ps

    module test;
    reg [30:0] in;
    wire [4:0] sum;

    FivebitWallace FW(
        .in(in),
        .sum(sum)
    );

    initial begin
        in = 31'b0;
    end

    always begin
        #100 in = 31'b1;
        #100 in = 31'b11;
        #100 in = 31'b111;
        #100 in = 31'b1111;
    
        #100 in = 31'b1_1111;
        #100 in = 31'b11_1111;
        #100 in = 31'b111_1111;
        #100 in = 31'b1111_1111;

        #100 in = 31'b1_1111_1111;
        #100 in = 31'b11_1111_1111;
        #100 in = 31'b111_1111_1111;
        #100 in = 31'b1111_1111_1111;  

        #100 in = 31'b1_1111_1111_1111;
        #100 in = 31'b11_1111_1111_1111;
        #100 in = 31'b111_1111_1111_1111;
        #100 in = 31'b1111_1111_1111_1111;

        #100 in = 31'b1_1111_1111_1111_1111;
        #100 in = 31'b11_1111_1111_1111_1111;
        #100 in = 31'b111_1111_1111_1111_1111;
        #100 in = 31'b1111_1111_1111_1111_1111;    

        #100 in = 31'b1_1111_1111_1111_1111_1111;
        #100 in = 31'b11_1111_1111_1111_1111_1111;
        #100 in = 31'b111_1111_1111_1111_1111_1111;
        #100 in = 31'b1111_1111_1111_1111_1111_1111;
    
        #100 in = 31'b1_1111_1111_1111_1111_1111_1111;
        #100 in = 31'b11_1111_1111_1111_1111_1111_1111;
        #100 in = 31'b111_1111_1111_1111_1111_1111_1111;
        #100 in = 31'b1111_1111_1111_1111_1111_1111_1111;   

        #100 in = 31'b1_1111_1111_1111_1111_1111_1111_1111;
        #100 in = 31'b11_1111_1111_1111_1111_1111_1111_1111;
        #100 in = 31'b111_1111_1111_1111_1111_1111_1111_1111;
    end

endmodule

本部分是用于仿真测试的 TestBench 文件，通过每延时 100 个时间单位改变寄存器数值为仿真提供逐位递增的仿真激励信号。

四、仿真过程与结果

在仿真过程中，遭遇了 ModelSim 的一系列玄学问题，遂换用 Vivado 完成本次实验的仿真。仿真时长为 3200 ns，得到了以下输出波形。

可以观察到仿真波形与预期一致，实现了三十一输入五输出的华莱士树加法器基本功能。

五、结论

本次实验通过由下至上逐级构建的思想与方法完成了三十一输入 5-bit 华莱士树加法器的设计，掌握了全加器和华莱士树加法器电路原理与 RTL 语言实现方式，巩固了 TestBench 的设计和编写方法。

但由于时间仓促，本次实验还有诸多可供完善之处：尚未在各个逻辑门中插入寄存器（D 触发器）实现流水线结构，可在每个串行进位加法器后插入以达到更好的电路延时，提高工作频率；串行进位加法器的设计方式过于冗余，可通过变量形式传入串行进位加法器位数，以简化代码结构；TestBench 文件撰写方式过于暴力美学，可以寻求更优雅的解决方式。